<HOME
<Rockets
Raketin_vakavuus
A model rocket simulation spreadsheet
(Don't worry, the thing is in English, despite the Finnish name.)
- Old version:
- New and improved:
Usage instructions
General
The table is colour-coded as follows:
|
Gray cells are for your input values
|
|
Yellow cells are the main calculated results
|
|
Pale yellow cells are intermediate or less important results,
which may or may not be of minor interest to the more nerdy types
|
|
Light blue cells are for parameters which you probably
won't need to or want to touch
|
|
White cells are used by raketin_vakavuus for its own
calculations, you will better maintain your sanity by ignoring these.
|
The table is divided into sections:
- Rocket definition: This is where you enter the data for all
the parts of the rocket, from nose cone to fins to internal payloads
- Calculated stability: Once you have defined the structure of
your rocket, its critical stability data are displayed here
- Wind stability: You decide how much stability you want to
maintain, and this section will calculate the maximum wind speed that you
can safely fly your rocket in
- Fin calculation: Define all elements of your rocket in the
rocket definition section except the fins. Then define here
how much stability you want, and it will tell you how big your fins must be.
- Added mass calculation: If you're happy with your rocket's
appearances but it's just not stable, then define here how much stability
you want, and it will tell you how much mass to add to the nose-cone.
Defining the rocket
There are currently five types of elements: nose, tube,
widen, fins and mass. The first element in the
rocket definition must be nose (that's why the cell is white, not
gray). The tube elements are assumed to be round and of uniform
thickness. Conical sections that join tubes of different thicknesses
are always widen-elements (even the ones that narrow the tube). The
mass-elements are for defining engines, engine mounts, parachutes,
payloads etc. which are inside the tube, and do not affect airflow. Any
bulging payload compartment must, of course, be defined with tube- and
widen-elements.
All elements are given a mass. The nose-, tube- and
widen-elements are given their length, whereas fins and
masses are given their position. The position is measured
relative to the "current position", i.e. to the bottom of the last
body-element (nose, tube, widen) defined. If
located e.g. on a tube already defined, then that relative position is
negative, otherwise positive (i.e. down is positive, up
negative). Other parameters for the elements are as follows:
- nose: diameter, shape (this can be ogive, cone,
parab or ellip)
and hollowness (enter 1 if hollow)
- tube: no other
parameters. Diameter is inherited from preceding nose- or
widen-elements.
- widen: new diameter (i.e. diameter of bottom
end). Old (top end) diameter is inherited from preceding nose- or
widen-elements.
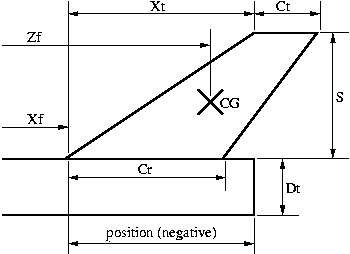
- fins: number of fins n, and geometry parameters
S, Cr, Ct and Xt (see figure). Note:
Fin calculations need to know the
diameter of the body tube the fins are attached to. This is inherited
from preceding elements, so you must first define the tube
section, then the fins (i.e. the fins' position will be
negative in almost all cases).
- mass: no other parameters.
Other parameters in this section are the angle of attack (alpha) and
K for Galejs stability calculations [2] and for the projection
method, the ratio of total fin area to projected fin area (k).
Calculated stability
The center of gravity can be calculated exactly. The center of pressure,
on the other hand, is approximated by three methods: Barrowman [1],
Galejs [2] and projection. The stability obtained by these three
methods is presented both in centimeters (difference between CG and
CP) and calibers (multiples of maximum body diameter). Positive is
stable, negative unstable.
Wind stability
This is calculated exclusively by the Galejs method, since it is the only
one to account for the effect of cross-winds on the body tube [2]. You
can enter the desired stability in either cm or calibers (the bigger value
will be used). The effect of wind is greatest at take-off when speed is
lowest, so this is calculated from enginge thrust and launcher height.
Since K depends slightly on the angle of attack, you can change it
accordingly, and if you are launching from the Moon, adjust the
g-constant as well.
Fin calculation
To calculate fins required to obtain a certain stability, do not define
any fins in the rocket definition -section (or you can just delete the
keyword "fins" and the current fins will be ignored).
In this section, you provide the number of fins n, the diameter of the
tube where they are attached (Dt, unlike in rocket definition, this is
not inherited from anywhere!), the areal density of the fin material in
grams per square centimeter (don't use 0 even for very light material,
instead use 0.00001 or such, to avoid a division by zero), and the fin's
geometry—these values will be scaled equally up or down, retaining the
fin's overall shape. Like above, the required stability can be entered
as cm or calibers, the larger of the two will be used. The position of
the fins is given in cm from the top of the rocket, measured to the
center of gravity of the wings, not their top edge as before!
For Galejs calculations, the alpha and K
values entered in the Rocket definition -section will be used.
The projection method has been solved analytically, whereas Barrowman and
Galejs approximations are performed in three iterations. The first two
results are visible in pale-yellow so you can see if the results are
converging correctly. The final dimensions S, Cr, Ct
and Xt of the fins
are calculated, as well as the position (from the top of the rocket) of
the fin's top edge (Xf). Fin areas and their mass contribution to the
rocket are also presented.
Added mass calculation
When the entire rocket (including fins) is defined in the first section,
you can enter here the required stability of the rocket (cm or calibers,
the larger will be used) and the position (from the top of the rocket)
where the mass can be added. The required mass and total rocket mass is
calculated based on all three methods.
References
- James S. Barrowman, Judith A. Barrowman,
The Theoretical Prediction of the Center of Pressure,
http://www.apogeerockets.com/education/downloads/Barrowman_report.pdf
- Robert Galejs,
Wind Instability—What Barrowman Left Out,
http://www.cmass.org/member/Robert.Galejs/sentinel39-galejs.pdf

